1. 一致性hash算法

Hash 算法也叫做散列算法，他可以让任意长度的数据M映射成为长度固定的值H。

Hash算法的作用

Hash算法的第一个作用就是数据的快速存储与查找。写过程序的人都知道，基本上主流的编程语言里面都有个数据结构叫做Map（dictionary或者 hash table）。它是根据key来直接访问结果的数据结构。key的种类多种多样，形式各异，怎么通过key来快速查找结果呢？如果将key通过一定的Hash算法变成通用一致的格式（索引），就可以实现这一功能。

同时，Hash算法也可以看做是一种加密算法，但是这个加密算法只有加密的过程没有解密的过程，是不可逆的。各种加密货币中的密钥体系或多或少都用到了Hash算法，其中比较有名的像：MD4，MD5，SHA-1，SHA-2，SHA-3等。除了加密货币，Hash的加密算法在文件校验，数字签名，鉴权协议等方面都有非常重要的作用。

Hash算法的冲突

根据Hash算法的定义，将任意长度的数据M映射成为固定长度的数据H(M)，因此肯定存在不同的key映射到同一个值的情况。作为密码算法的Hash算法主要关注的是散列函数是否均匀，而作为存储和查找的Hash算法则同时需要关注当产生冲突时候的解决办法。

一致性hash算法

在分布式系统中，如果数据是存储在很多个节点中，由于节点的状态是不稳定的，可能新增节点也可能随时有节点下线。可以参考P2P下载网络，节点的个数和在线时间都是不稳定的。如何在这样的不稳定的环境中保证数据的正确命中，不会因为节点个数的增减而导致大部分数据的失效，这就是一致性Hash算法需要解决的问题。

1. 算法是否均匀 算法均匀是指使用这样的算法，不同的key计算出来的结果是均匀的，不会出现集中分布的情况，这个是Hash算法的基本要求，大多数Hash算法都能做到。

2. 算法是否单调 算法是否单调是指，在新增数据节点之后，需要进行数据的重新分配，但是这种数据的分配只会出现在将现有节点的数据转移到新增节点之上，而不会出现将现有节点的数据转移到老数据节点的情况。这样的好处就是尽量保证现有数据的位置不变，从而减少数据再分配过程中对系统性能的消耗。

3. 分散性 在分布式环境中，由于网络的原因，并不是每个节点都能够获取到完整的全节点信息，那么在做数据散列的时候，有可能因为获取到的全节点信息不同而导致得出不同的散列结果，这也是好的一致性算法应该要解决的问题。

一致性hash算法的原理

一致性Hash算法是在1997年由麻省理工学院提出的一种分布式hash实现算法。简单点说就是使用常用的hash算法将key映射到一个具有2^32^次方个桶空间中，即0-(2^32^-1)的数字空间中。我们可以将其用一个首尾相连的闭合环形表示，如下图所示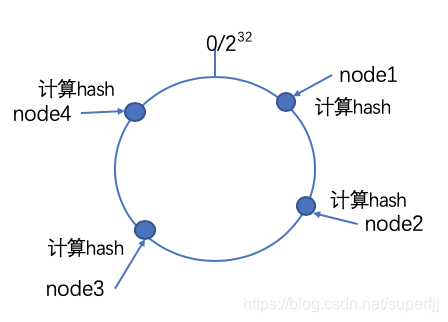： 图中列出了一个虚拟的圆环，上面有0-2^32^个节点位置。算法首先需要计算出存储节点在圆环上的位置。具体可以选择服务器的ip或主机名作为关键字进行哈希，这样每台机器就能确定其在哈希环上的位置。这一点是为了保证算法的分散性：节点的位置跟具体多少个节点没关系，只跟节点的内在特性有关系。

上图我们假设有4个节点：node1，node2，node3，node4。计算好他们的位置之后，接下来我们就需要就计算出各个不同的key的存储位置了：将key用同样的算法计算出hash值，从而确定其在数据环上的位置，然后从此位置沿着逆时针行走，遇到的第一个服务器就是该数据应该存储的节点。

如下图所示，我们有A，B，C，D四个数据对象，经过hash计算之后，其在图中的位置和应该存在的节点位置如下：

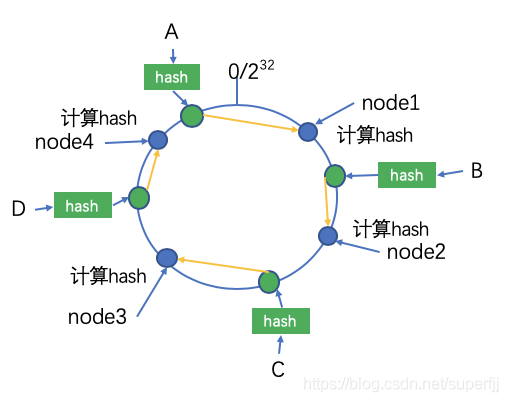其中A存储在node1节点，B存储在node2节点，C存储在node3节点，D存储在node4节点。

容错性

下面我们考虑下节点挂掉的情况，如下图所示，当node4节点挂掉之后，按照一致性hash算法的原则，A，B，C存储节点不做任何变化，只有D节点会重新存储到node1 上。如下图所示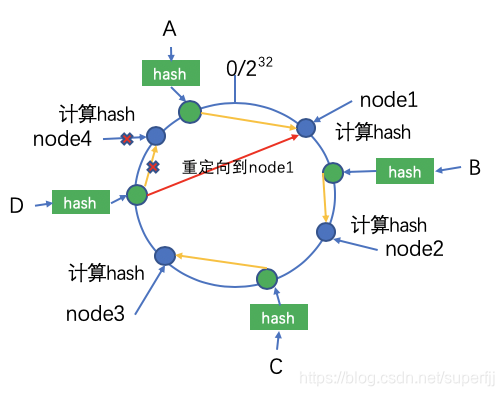： 同样的，假如我们添加了一个node5节点，其hash值在C和node3之间，则只有C的存储位置需要转移。如下图所示： 由此可见，一致性hash算法在系统节点变化的时候，只需要重定向一小部分数据的存储位置，具有较强的容错性和可扩展性。

虚拟节点

当系统中节点很少的情况下，或者现有的节点计算出来的Hash值比较接近的情况下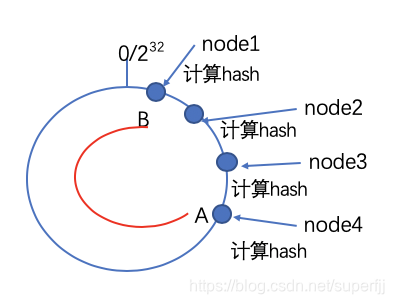， 如上图所示，所有A-B这一段路径上的数据都会存储在node1上面，很明显这会导致node1上面数据过多，不满足系统分散性的需求。解决办法就是我们可以创出一下虚拟节点，即对每一个服务节点计算多个哈希，每个计算结果位置都放置一个此服务节点，如下图所示：

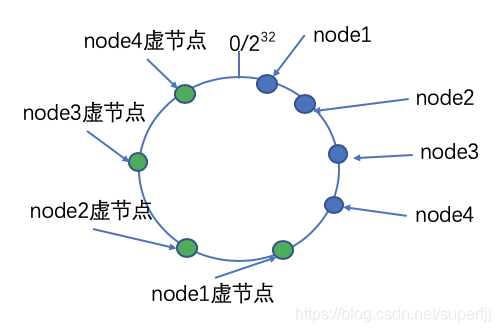这样就可以解决数据倾斜的问题。

更多教程请参考 flydean的博客