跳到主要内容

18. 树状数组-BIT-Fenwick Tree

简介

Fenwick Tree也叫做树状数组，或者Binary Indexed Tree(BIT),是一个查询和修改复杂度都为log(n)的数据结构。主要给定区间，求最值，或者求和。

接下来我们来具体讲解一下Fenwick Tree的概念。

什么是Fenwick Tree

如果我们有一个数组，我们希望很方便的进行下面的几个操作：

  1. 统计该数组前n个元素的和。
  2. 统计该数组从n到m中间元素的和。
  3. 很方便的对该数组中的某个元素进行add。

为了实现上面的3个问题，该怎么构建这个数据结构呢？

一个很简单粗暴的想法就是构建一个数组，这个数组第n个元素，是原数组的前n个元素的和。

如果构建了这样的数组，那么1，2两个操作是很容易满足的。

但是对于操作3来说，更新了某一个元素，需要级联的对其后的所有元素进行更新，这样操作的时间复杂度是O(n)。

如果对于数组的更新很少的话，这种数据结构是合适的，但是当数组更新比较多的情况下，我们就需要一个更加高效的方式了。

还记得java中有一个LinkedSkipList，它采用的是空间换时间的办法来加快链表的查询。

同样的，我们可以适当的牺牲操作1和操作2的时间复杂度，从而达到提升操作3的目的。

也就是说，我们可以构造出一些分层的结构，从而对操作3进行优化。

好了，那么Fenwick Tree到底是什么呢？

Fenwick Tree是一个和原始数组等长的数组，其中新的数组中的每个元素表示的都是原始数组中某个范围元素的和。

为了方便用数学语言的表示，这里我们假设数组的元素是从index=1开始。也就是说index=0的值为无效。

我们用一张图来表示：

上面的就是原数组，下面的是新构建的BIT数组。

其中BIT数组中的1是原数组中1-1的和，2是原数组中1-2的和，2是原数组中3-3的和，4是原数组中1-4的和。

看起来好像没什么规律，其实规律是有的。我们接下来详细讲解。

Fenwick Tree的创建

在介绍Fenwick Tree的创建之前，我们先来介绍一个bit操作：

 private int lowBitOne(int S) { return (S & (-S)); }

上面的操作是对一个整数，求得它和它的负数的按位与。

我们以13为例举个例子：

13的二进制表示是Ox1101, -13的二进制表示是1101按位取反后再加1，也就是0x0011。

所以 13 & -13 = Ox1101 & 0x0011 = 0x0001 = 1

这个值表示的是13中低位1加后面的0代表的值。

这个值有什么用呢？

当我们向原数组的某个index添加某个值的时候，我们使用S + (S & (-S)) 来表示下一个要添加的index，也就是该index的父节点。

    // 构造FenwickTree，更新相应的值
    void update(int i, int v) {
        for (; i < ft.size(); i += lowBitOne(i)){
            ft.set(i, ft.get(i)+v);
        }
    }

举个例子：

当我们向原数组的index=1 添加100的时候。

首先我们将构建的Fenwick Tree，index=1加上100，然后计算 i += lowBitOne(i)=2，也就是说将index=2的元素添加100，接着计算i += lowBitOne(i) = 4 ，以此类推，直到i的范围超出了数组的长度。

这也就是为什么BIT数组中的1是原数组中1-1的和，2是原数组中1-2的和，2是原数组中3-3的和，4是原数组中1-4的和的原因。

根据上面的更新规则，我们可以使用S + (S & (-S))得到一个虚拟的树形结构，给定某个i，其父节点的index=i+（i & -i）。

我们来看一个创建Fenwick Tree的动画：

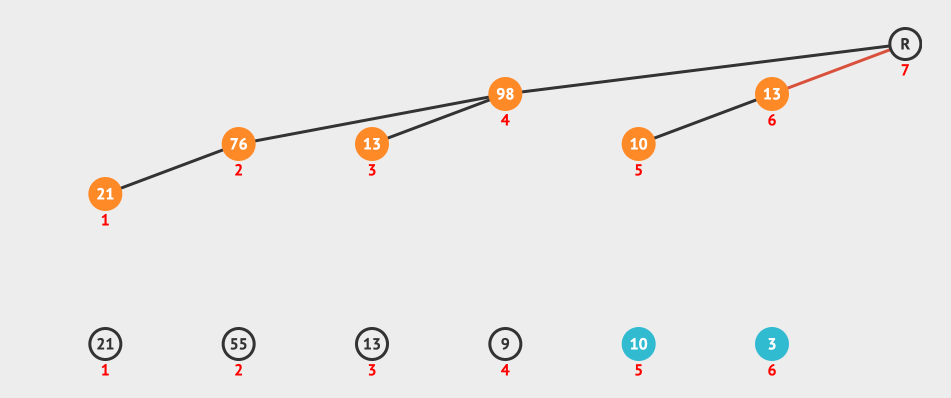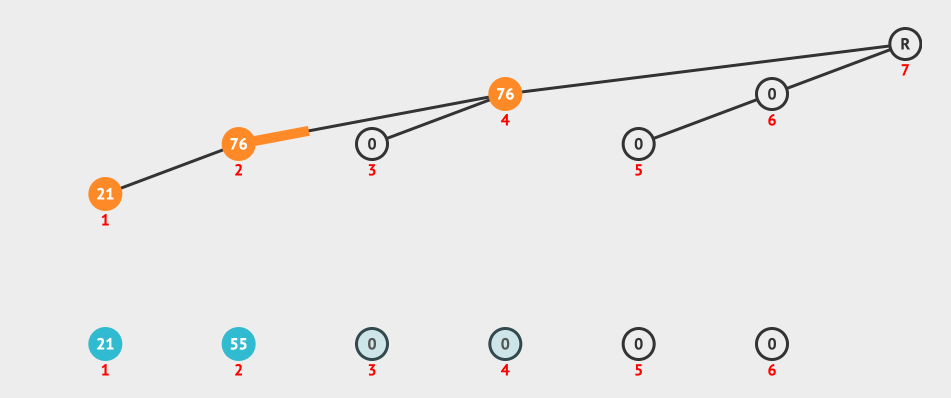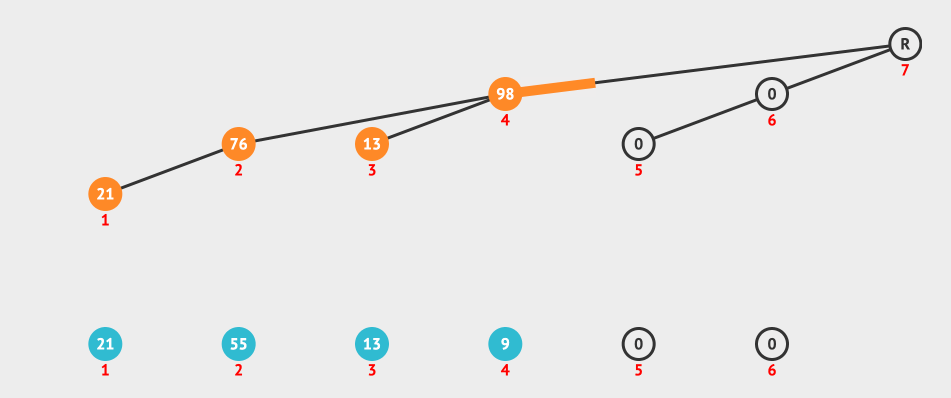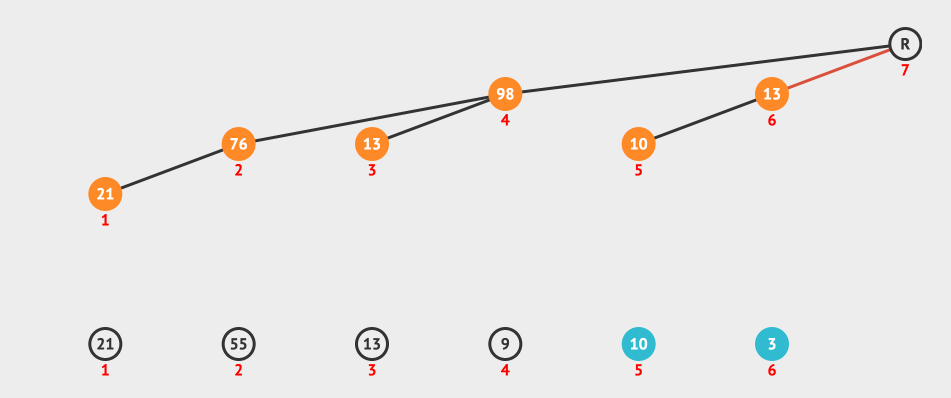
上面的动画就是按照i+（i & -i）构造出来的树形结构进行更新的。

构造Fenwick Tree的父子关系还可以简单的表示为下面的图：

Fenwick Tree的查询

上面我们在创建的时候，是根据i+（i & -i）来构造父子节点关系。

那么查询的时候呢？

考虑一下，假如我们想要查找index 1 to 13范围的元素的和，应该怎么去做呢？

将13变成二进制是Ox1101 = Ox1000 + Ox100 + Ox1, 也就是说Range(1,13)= Range(1,8)+ Range(9, 12) + Range(13, 13)来表示。

根据我们上面的创建BIT树的图，我们可以知道Range(1,8) ， Range(9, 12)， Range(13, 13) 的值可以刚刚好分别用BIT[8], BIT[12], BIT[13] 来表示。

但是用创建BIT树时用的图好像不太好找到这三者的关系。

于是我们使用i -（i & -i）来重新构造查询节点的父子关系图如下：

要想获得BIT[13]的值，只需要依次找到13的父节点，累加就行了。13的父节点是12，8，于是我们很轻松的找到了要查找的结果。

相应的java代码如下：

    public int rangeSumQuery(int j) {                              // 范围查询 1 - j
        int sum = 0; for (; j > 0; j -= lowBitOne(j)) {
            sum += ft.get(j);
        }
        return sum;
    }

    public int rangeSumQuery(int i, int j) {                       // 范围查询 i - j
        return rangeSumQuery(j) - rangeSumQuery(i-1);
    }

最后上一个动画图，看一下查询的过程：

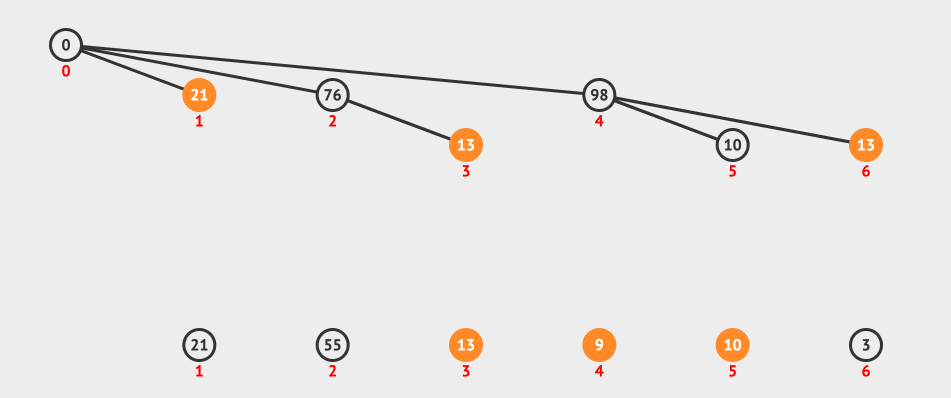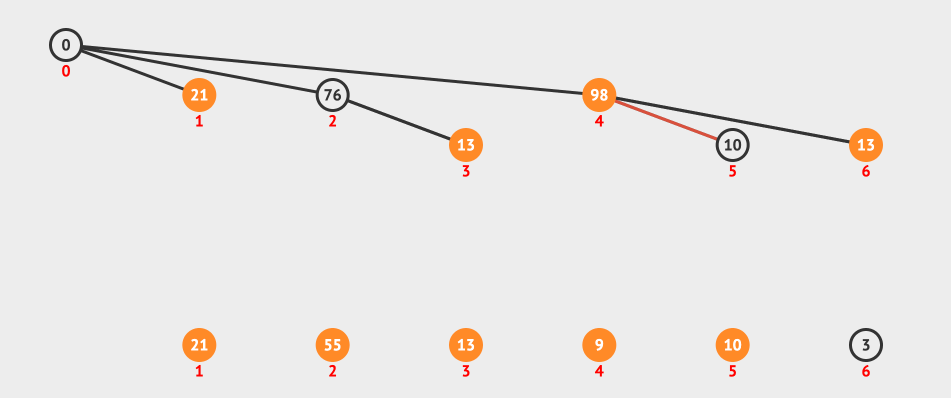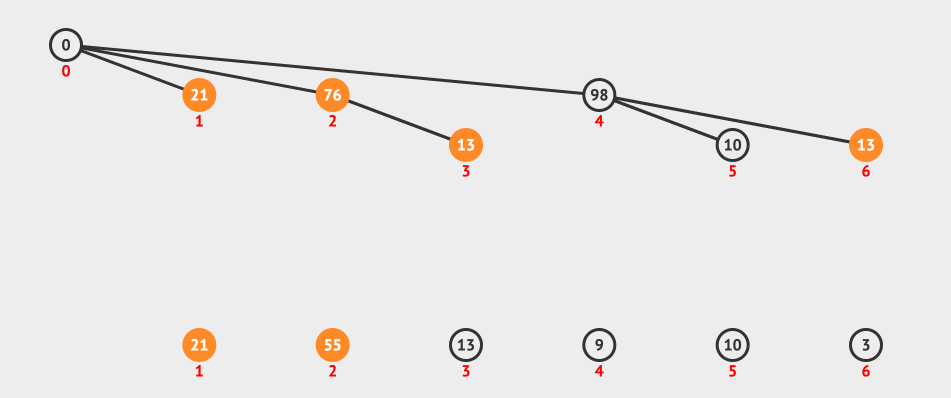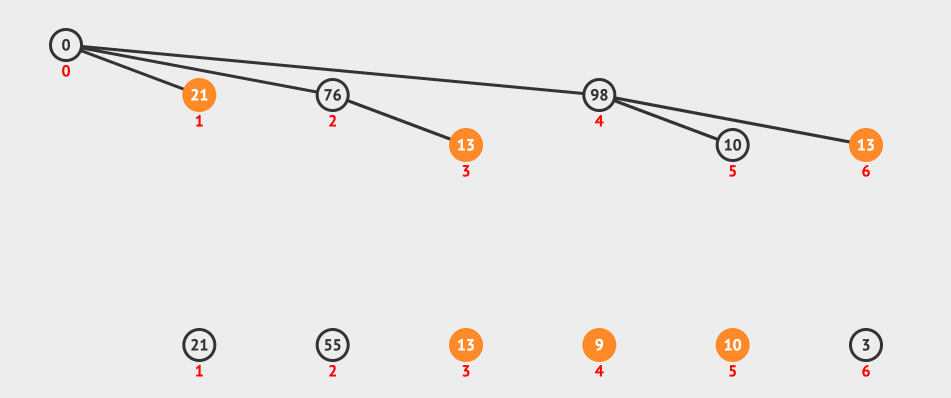
上图我们表示的是一个范围查询3-5,所以我们的流程是找到5这个节点，然后找到5的父节点4，4的父节点是0，我们忽略。

然后找到3-1=2的节点和它的父节点，最后两个sum相减就得到了我们要的结果。

总结

Fenwick Tree本质是一个和原数组一样长度的sum数组，根据插入和查询的方式不同，可以组建成不同的数状结构。

根据树状结构来获得父子节点的关系，从而进行范围的查找和更新。

本文的代码地址：

learn-algorithm

本文收录于 www.flydean.com

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！


点我查看更多精彩内容:www.flydean.com关注公众号加我好友
Loading Comments...